“顶点覆盖问题 NP-Complete 证明”

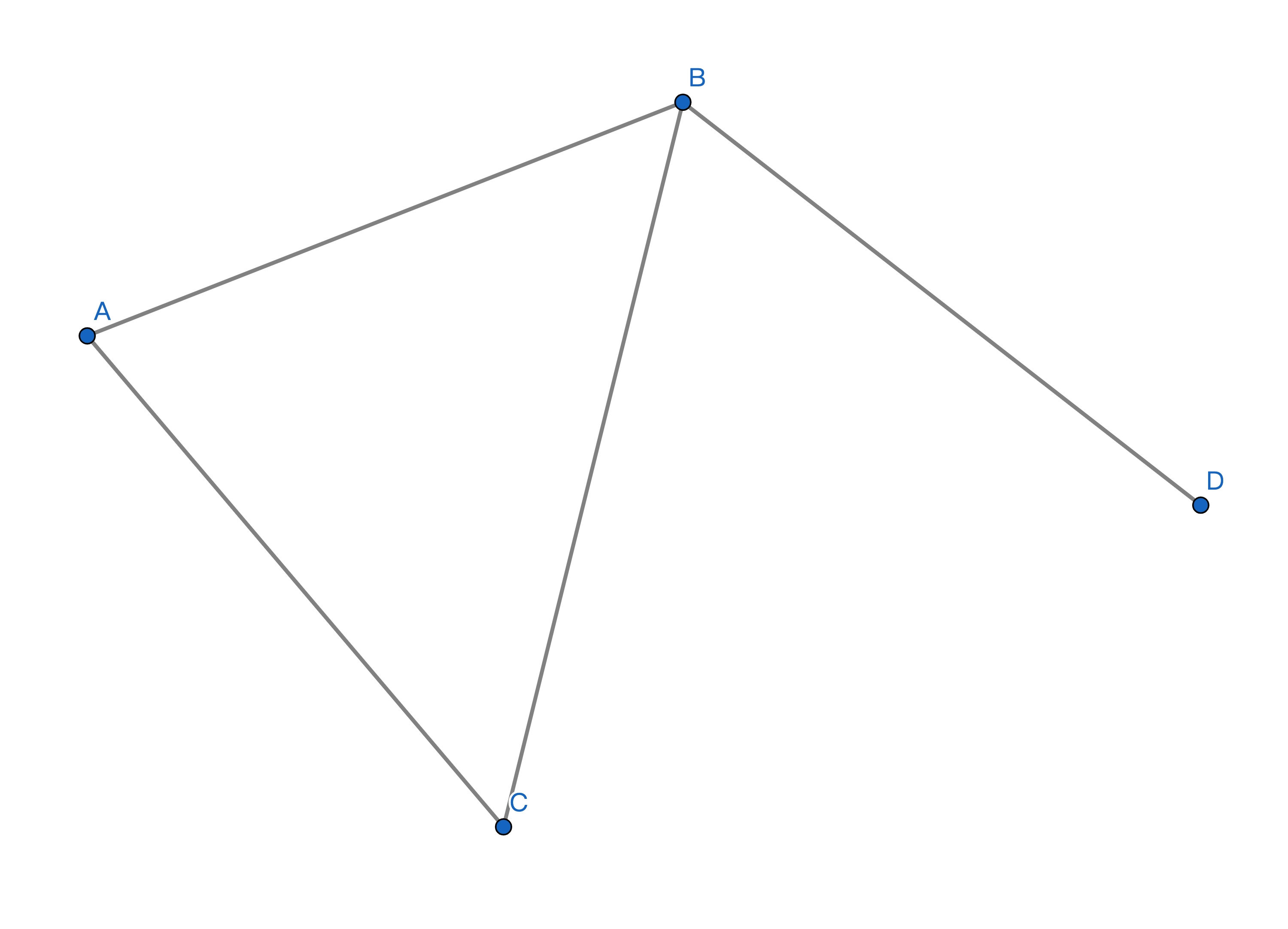
顶点覆盖问题（Vertex Cover）的描述如下：给定 ，其中 是一个无向图，问图中是否存在点集 ，， 使得 中的每一个顶点覆盖 中所有的边。即 中每一条边的起点或终点都为 中的一个点。以下图为例， 就是一个符合条件的点集，因为图中的 4 条边，每一条边都连接了 中至少一个点。

为了证明其 NP 完全，我们首先还是证明其是 NP 问题。给定一个 和一个 ，我们只需要遍历 中的每一个边，检查其是否与 中一个点相连，即可判定 的正确性。显然这个过程是可以在多项式时间内完成了，所以顶点覆盖问题是一个 NP 问题。

接下来，为了证明其是 NP 难问题，我们将 3-SAT 归约到顶点覆盖问题。3-SAT 的形式如下：

那么给定一个 3-SAT 表达式，我们作一下操作：

1. 将每一个簇中的三个变量相互连接。
2. 将不同簇中不一致的相同变量相连。 不一致的意思是，存在两个不同簇的相同变量 和 ，若 为真，则 为假；若 为假，则 为真。

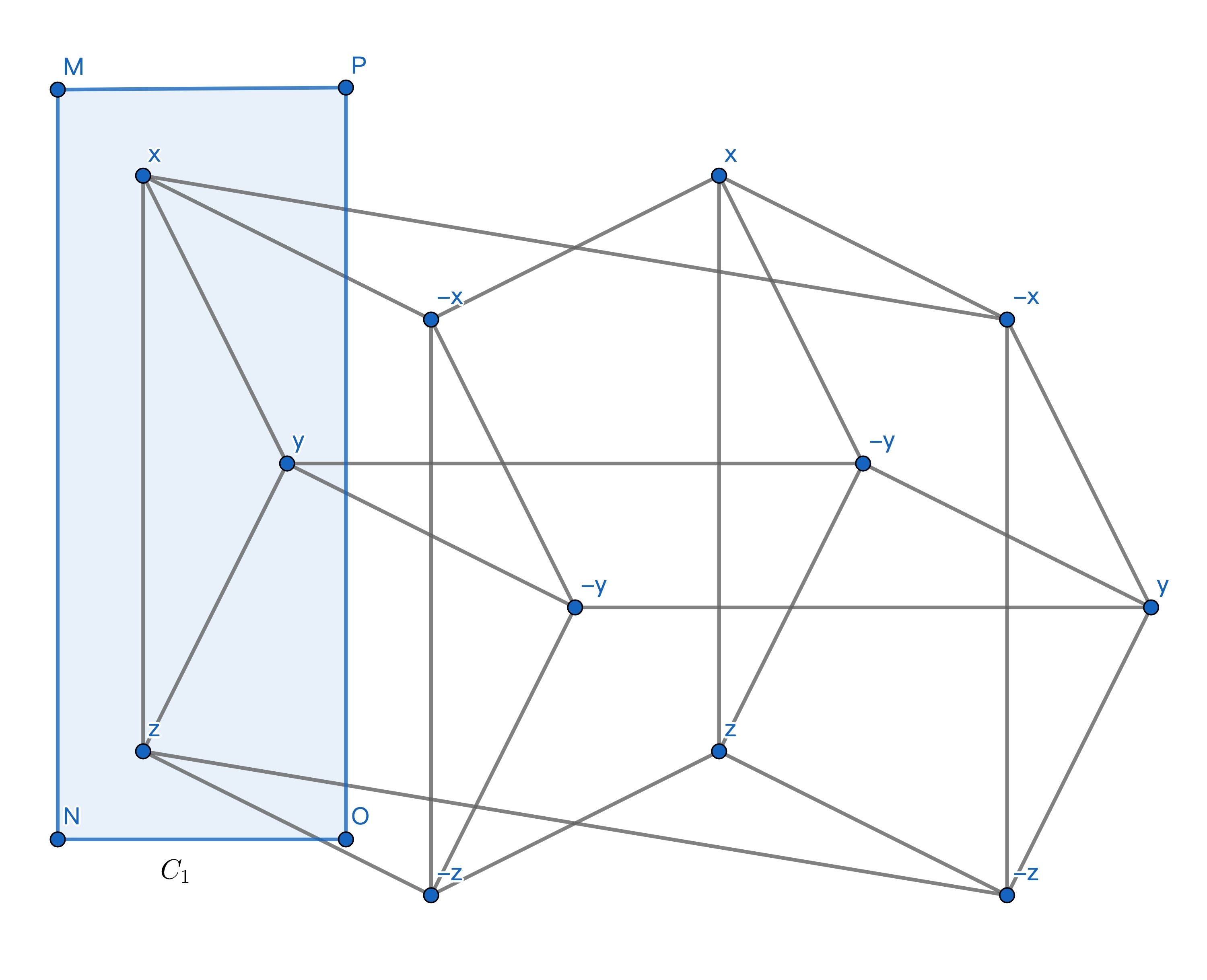
这样我们就把一个 3-SAT 布尔表达式转换成了图，且 ， 是布尔表达式的簇数。举一个例子，例如一个 3-SAT 布尔表达式为 ：

则其按照上述规则，对 作出的图为：

现在，我们还是来证明两个问题：

（1）若已知一个 3-SAT 问题有解，则其转换后的图 在顶点覆盖问题上也有解。因为我们有一个 3-SAT 有解，即 。那么对于这个 3-SAT 中每一个簇都至少有一个变量为真。我们取除这个变量外的另外两个变量为顶点覆盖问题中 的成员，最后一共可以得到 个成员。由于对于每一簇而言，转换后在图中构成了一个三角形，所以从三角形的 3 个顶点中选出两个顶点必然会包含该三角形所有的边。另一方面，对于每一个变量，其都有与其矛盾的不在一个簇的相同变量相连了。所以只要 3-SAT 问题有解，则对于每一个变量，不管其取值如何，都必然与与其相矛盾的相同变量连接（例如不管 取真还是取假，都会与 相连）。所以 在 一定满足，只要对应的 3-SAT 问题满足。

（2）若已知一个顶点覆盖问题 ，其转换后的 3-SAT 也有解。 我们可以将 通过上述规则逆向转换为布尔表达式，且将 中不属于 的顶点所对应的变量取真，则 3-SAT 问题为真。

综上所述，我们将 3-SAT 问题归约到了顶点覆盖问题。所以顶点覆盖问题是 NP 完全的。