引1：一道题

Problem:在4*4的棋盘上，摆有15个棋子，每个棋子分别标有1-15的某一个数字。棋盘中有一个空格，空格周围的棋子可以移到空格中。现给出初始状态和目标状态，要求找到一种移动步骤最少的方法。

input:第一行是整数n, 表示有多少组输入数据。 每组数据有 4 行，每行 4 个数字，表示该行各列棋子的标号。数字 0 表示空格。各组数据间用空行分割。每组数据的目标状态均为



1
2
3
4



 1  2  3  4
 5  6  7  8
 9 10 11 12
13 14 15  0

output:输出由 n 行整数组成。 第 i 行数字表示对于第 i 组初始棋盘，需要移动的最少步骤。 （注：测试数据中的所有初始棋盘状态都可以到达目标状态）

samples



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16



Input
2

 1  2  3  4
 5  6  7  8
 9 10 11  0
13 14 15 12

 1  2  3  4
 5  6  7  8
 9 10  0 11
13 14 15 12

Output
1
2

什么是 IDA*1

类似于 Dijstra 算法可以计算两点之间的最段路径，IDA*算法可以计算两种状态下由 A 状态转换到 B 状态的最短路径。这个算法之前大量活跃于各种拼图游戏，比如 Windows7 桌面小程序拼图的还原过程，就使用到了这个算法。现在这个算法大量应用于深度学习方面，为深度学习的进程做了很大的优化。

为了更好的讲解这个算法，首先请读者先读懂引1的题目。其实引1的题目归纳一下就是给你一个 4x4 的棋盘， 0 表示空格，大于 0 的表示拼图，每次只能有一个相邻空格的拼图和空格交换位置，问最后至少要多少步才可以从初始状态转换到目标状态。我们可以从下面 3x3 的棋盘的还原过程中类比。



1
2
3
4



   1  3        1     3        1  2  3        1  2  3        1 2  3
4  2  5   =>   4  2  5   =>   4     5   =>   4  5      =>   4 5  6
7  8  6        7  8  6        7  8  6        7  8  6        7 8
initial        1 left          2 up          5 left         goal

很明显的一道搜索问题，那么问题就是我们要使用 BFS（广度优先搜索）还是 DFS （深度优先搜索）呢？我们使用 DFS， 因为 BFS 就是 A* 算法了，我们这篇主要讲的是 IDA* 如何优化 DFS。

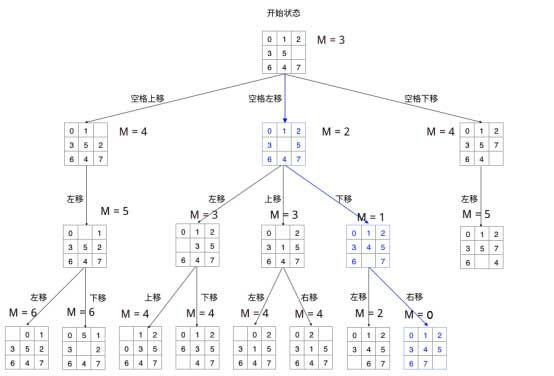
对于每一步，空格都有上下左右等多种选择，如果每一步的权重是相等的，那么我们的复杂度将称指数上升。 n 层就会有 4^{n} 种情况。如何剪掉多余的枝，将蓝色路径显现出来，是这个算法的关键。

对于 DFS 算法的过程而言，我们希望他继续搜索的是有希望得到正确答案的方向，而不是错误的方向。如何评估目前状态的希望度呢？有两种方法：

  1. Hamming 优先级函数: 错误位置方块的数量，加上到达本搜索节点时移动的次数。直观地说，一个有少量错误位置方块的搜索节点更接近于目标，我们更希望使用移动次数较少就可以到达的搜索节点。
  2. Manhattan 优先级函数: 方块与它们目标位置的 Manhattan 距离的总和（垂直距离与水平距离的总和），加上到达本搜索节点时移动的次数。

这里我们只考虑 Manhattan 的优先度。

假如让拼图上的每个方块都可以穿过邻近方块，无阻碍地移动到目标位置，那么每个不在正确位置上的方块它距离正确位置都会存在一个移动距离，这个非直线的距离即为曼哈顿距离 (Manhattan Distance) ，我们把每个方块距离其正确位置的曼哈顿距离相加起来，所求的和可以作为搜索代价的值，值越小则可认为状态越优秀。

f\left( n\right) =g\left( n\right) +h\left( n\right)

f\left( n\right) 是一开始预估的深度

g\left( n\right) 是目前的深度

h\left( n\right) 是预估目前状态到目标状态的深度

在每次生成子状态结点时，子状态的 g\left( n\right) 值应在它父状态的基础上 +1，以此表示距离开始状态增加了一步，即深度加深了。所以每一个状态的g值并不需要估算，是实实在在确定的值。 影响算法效率的关键点在于 h\left( n\right) 的计算，采用不同的方法来计算 h\left( n\right) 值将会让算法产生巨大的差异。

对于 IDA* 算法而言，你对 f\left( n\right) 预测的越准确，那么程序越快。所以 IDA* 是采用深度迭代的方法来预测 f\left( n\right) 的，即先找到一个 f\left( n\right) 的最小值，这个最小值是最理想状态下初始状态到达目标状态的步数，即初始状态下的的曼哈顿距离。然后对这个 f\left( n\right) 做 DFS，如果找到了就输出结果，没有找到就 f\left( n\right) =f\left( n\right) +1 ，再做 DFS，直到找到为止。可以看得出在深度迭代的时候，会做很多次重复运算，比如我的 f\left( n\right) 开始为 20 没找到，开始找 f\left( n\right) = 21 的时候，前面的 20 次迭代是上次算过的，重复运算了。

但是因为 DFS 每加深一层复杂度称指数型上升，所以当 f\left( n\right) = 21 的时候，前面 20 次迭代运算加起来的时间还没有最后一次迭代的时间多，所以重复运算的时间只占了整个运算相当少的时间，可以被省略掉。

所以整个程序流程如下：

LOOP
DFS
From Position Of The Blank
x > 0
x < 3
y > 0
y < 3
Yes, Continue To Search Until Match Goal
No, This Direction Can Not Find the Result
Yes And Match The Goal
Fx = Fx + 1
DFS
Loop
Fx >= Gx + Current Depth?
Current Gx is The Sum Of The Current Situation's Manhattan Distance
Return
Found
Move Left
Move Right
Move Up
Move Down
Start
Input
Predicted Fx Is The Sum Of The Root's Manhattan Distance
Problem Solved

CPP 程序参考



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142



#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int position[16][2]={ {3,3},{0,0},{0,1},{0,2},{0,3},{1,0},{1,1},{1,2},{1,3},{2,0},{2,1},{2,2},{2,3},{3,0},{3,1},{3,2} };

inline int getDistance(int x1, int y1, int x2, int y2){
	return abs(x2 - x1 + y2 - y1);
}

class table{
public:
	short list[4][4];
	int blankx, blanky;
	inline void setblank(int x, int y){
		this->blankx = x;
		this->blanky = y;
	}
	inline int getblankx(){
		return this->blankx;
	}
	inline int getblanky(){
		return this->blanky;
	}

	inline bool equal(const short w[4][4]){
		for (int i = 0; i < 4; ++i) {
			for (int j = 0; j < 4; ++j) {
				if (this->list[i][j] != w[i][j]) {
					return false;
				}
			}
		}
		return true;
	}
	inline short * const operator[](const int i){
		return list[i];
	}
	table * const operator=(const table t){
		for (int i = 0; i < 4; ++i) {
			for (int j = 0; j < 4; ++j) {
				this->list[i][j] = t.list[i][j];
			}
		}
		this->blankx = t.blankx;
		this->blanky = t.blanky;
		return this;
	}
	inline int getManhattanDistance(){
		int sum = 0;
		for (int i = 0; i < 4; ++i) {
			for (int j = 0; j < 4; ++j) {
				if (this->list[i][j] != 0){
					sum += abs(i - position[this->list[i][j]][0])+abs(j - position[this->list[i][j]][1]);
				}
			}
		}
		return sum;
	}
};

int n, maxLimit, m;
short goal[4][4] = { {1,2,3,4},{5,6,7,8},{9,10,11,12},{13,14,15,0} };
bool has_found = false;
table tb, temptable;

void move_blank(table t, int d, int pre_d, int depth);

void DFS(table t, int depth, int pre_d){
	if (has_found) return;
	if (t.equal(goal)) {
		has_found = true;
		maxLimit = depth;
		return;
	}
	if (depth > maxLimit) return;
	int blankx = t.getblankx(), blanky = t.getblanky();
	if (blanky > 0)
		move_blank(t, 1, pre_d, depth);
	if (blanky < 3)
		move_blank(t, -1, pre_d, depth);
	if (blankx > 0)
		move_blank(t, 2, pre_d, depth);
	if (blankx < 3)
		move_blank(t, -2, pre_d, depth);
}

void move_blank(table t, int d, int pre_d, int depth){
	if (d + pre_d == 0) return;
	temptable = t;
	int blankx = temptable.getblankx(), blanky = temptable.getblanky(), tx = 0, ty = 0;
	switch (d) {
		case 1:
			tx = blankx; ty = blanky - 1;
			break;
		case -1:
			tx = blankx; ty = blanky + 1;
			break;
		case 2:
			tx = blankx - 1; ty = blanky;
			break;
		case -2:
			tx = blankx + 1; ty = blanky;
			break;
	}
	temptable[blankx][blanky] = temptable[tx][ty];
	temptable[tx][ty] = 0;
	temptable.setblank(tx, ty);
	if (temptable.getManhattanDistance() + depth <= maxLimit && !has_found) {
		DFS(temptable, depth + 1, d);
		if (has_found) return;
	}else{
		m = min(m, temptable.getManhattanDistance() + depth);
	}
}


int main(){
	ios::sync_with_stdio(false);
	cin >> n;
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < 4; ++j) {
			for (int k = 0; k < 4; ++k) {
				cin >> tb[j][k];
				if (tb[j][k] == 0) tb.setblank(j, k);
			}
		}
		has_found = false;
		maxLimit = tb.getManhattanDistance();
		while (!has_found && maxLimit <= 100) {
			m = 100000;
			DFS(tb, 0, 0);
			if (!has_found) {
				maxLimit++;
			}
		}
		cout << maxLimit << endl;
	}
}

  1. According to the Wikipedia, Iterative deepening A* (IDA) is a graph traversal and path search algorithm that can find the shortest path between a designated start node and any member of a set of goal nodes in a weighted graph. It is a variant of iterative deepening depth-first search that borrows the idea to use a heuristic function to evaluate the remaining cost to get to the goal from the A search algorithm. Since it is a depth-first search algorithm, its memory usage is lower than in A, but unlike ordinary iterative deepening search, it concentrates on exploring the most promising nodes and thus does not go to the same depth everywhere in the search tree. Unlike A, IDA* does not utilize dynamic programming and therefore often ends up exploring the same nodes many times. While the standard iterative deepening depth-first search uses search depth as the cutoff for each iteration, the IDA* uses the more informative f\left( n\right) =g\left( n\right) +h\left( n\right) , where g\left( n\right) is the cost to travel from the root to node n and h\left( n\right) is a problem-specific heuristic estimate of the cost to travel from n to the goal. The algorithm was first described by Richard Korf in 1985 ↩

本文作者 Auther：Soptq

本文链接 Link： https://soptq.me/2019/05/09/IDAstar/

版权声明 Copyright： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明出处。 Content on this site is licensed under the CC BY-NC-SA 4.0 license agreement unless otherwise noted. Attribution required.


发现存在错别字或者事实错误？请麻烦您点击 这里 汇报。谢谢您！