很久很久以前,当计算机还不普及的时候,对一个复杂函数的求导一定是众多学者的噩梦之一。试想,也许面对一个三元多项式函数时,你还可以游刃有余地对每一个变量求导数,但当函数被拓展到成千上万元、成千上万项的时候,你还有信心求的出来导吗?于是,随着计算机的普及,自动求导算法的提出帮助众多学者从大型函数的求导中解放了出来。
深度学习的反向传播也是一个典型的自动求导过程,而作为 pytorch 魔法力量的核心 Autograd,一定也被很多人好奇过其实现的原理。在本篇文章中,我将向大家解释一个最为简单的自动求道例子,希望可以抛砖引玉,启发大家。
自动求道的原理
每一个人在大一学习高等数学时,一定都听说过一个名词:链式法则。链式法则的数学表示如下:
可以看到, 是包含了 的函数, 是包含了 的函数,那么为了求到 对 的导数, 我们可以先求 对 的导数 , 然后求 对 的导数 ,最后把两个导数相乘就算出了我们想要的结果。
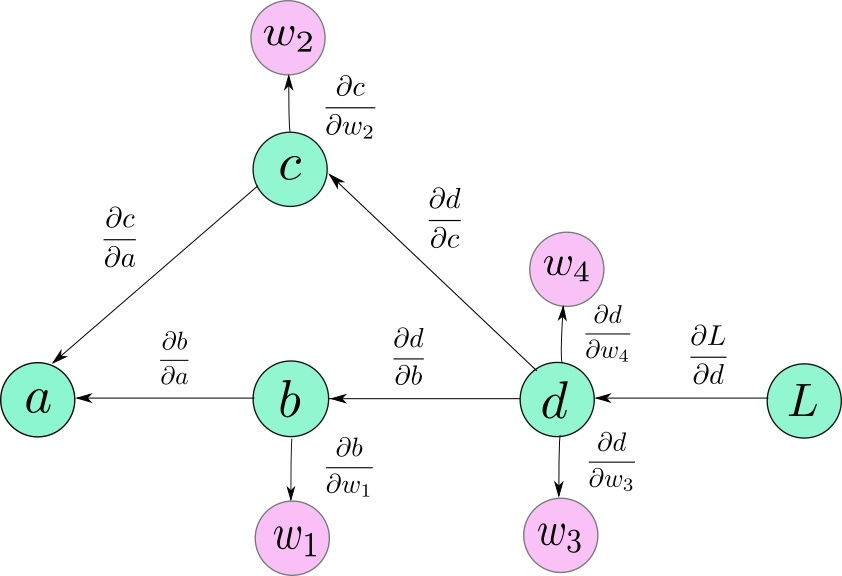
有人说,反向传播就是链式法则的另外一个花哨的名字。确实,这其实就是自动求导的核心。链式法则告诉我们,面对一个复杂的函数,我们若是可以把它拆分为一节一节简单的函数原子复合起来的结果,那我们对每一个简单的函数原子求导,最后把导数乘起来就可以得到复杂函数的结果。那么,深度学习最基础的神经元, 是不是就是一个简单的原子?
所以,自动求导和思路也就清晰了。我们通过前向传播记录每一个变量到最终函数的路径,然后我们沿着这条路径从函数返回,就可以得到函数对该变量的导数了。
利用二叉树设计一个自动求导机
在本部分我们将利用二叉树设计一个最简单的自动求导机。我们假设对一个简单的函数求导:
将算式转换为后缀表达式
上述函数为一个中缀表达式。中缀表达式是一种方便人类认知的表达式,但其不方便计算机读取。为了让计算机得到这个函数的解析树,我们需要先使用调度场算法将函数从中缀表达式转换为后缀表达式。
将后缀表达式转换为解析树
将后缀表达式转换为解析树就是一个非常简单的过程了,我们只需要对后缀表达式作一次遍历即可。遍历的规则如下:
- 当读取到的不为运算符时,将读取的字符作为解析树的一个节点存入栈内。
- 当读取到的为运算符时,将读取的字符作为解析树的一个节点,取出栈顶的两个节点作为其的左右子节点,然后存入栈内。
例如我们有一个表达式为 ,他所对应的后缀表达式为:
1
3 4 2 * 1 5 − 2 3 ^ ^ / +
于是我们构建解析树的过程如下:
| 输入 | 栈 |
|---|---|
| 3 | (3) |
| 4 | (3),(4) |
| 2 | (3),(4),(2) |
| x | (3),(4 x 2) |
| 1 | (3),(4 x 2),(1) |
| 5 | (3),(4 x 2),(1),(5) |
| - | (3),(4 x 2),(1 - 5) |
| 2 | (3),(4 x 2),(1 - 5),(2) |
| 3 | (3),(4 x 2),(1 - 5),(2),(3) |
| ^ | (3),(4 x 2),(1 - 5),(2 ^ 3) |
| ^ | (3),(4 x 2),((1 - 5) ^ (2 ^ 3)) |
| / | (3),((4 x 2) / ((1 - 5) ^ (2 ^ 3))) |
| + | (3 + (4 x 2) / ((1 - 5) ^ (2 ^ 3))) |
代码大概是这样的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct ParseTree{
string data; // 存的数据
int result = -1; // 子树计算的结果
int diff = -1; // 自动求导值
struct ParseTree* left = nullptr;
struct ParseTree* right = nullptr;
};
ParseTree* parse(){
for (int I = 0; I < o_vector.size(); I++){
if (isOperator(o_vector[I])) {
ParseTree* s1 = parse_stack.top();
parse_stack.pop();
ParseTree* s2 = parse_stack.top();
parse_stack.pop();
ParseTree* parseNode = new ParseTree();
parseNode->data = o_vector[I];
parseNode->left = s1;
parseNode->right = s2;
parse_stack.push(parseNode);
} else {
ParseTree* parseLeaf = new ParseTree();
parseLeaf->data = o_vector[I];
parse_stack.push(parseLeaf);
}
}
return parse_stack.top();
}
正向传播
我们得到的解析树之后,根节点就相当于是函数本身,内节点相当于是每一个计算符号,叶节点相当于每一个变量。正向传播的过程,实际就是从叶节点开始,经过每一个内节点最后计算到根节点的过程。由于二叉树的特点,每一个节点只有两个字节点,也就是说每一次内节点只会涉及一个符号,两个变量。所以整个正向传播过程就是从根节点的一个递归过程。
1
2
3
4
5
6
7
int calculate(ParseTree* head) {
if (head->left != nullptr || head->right != nullptr) { // head is a node
head->result =node_calculate((head->data)[0], calculate(head->left), calculate(head->right)); // node_calculate() is a function to calculate the result
return head->result;
}
return stoi(head->data);
}
反向传播
我们正向传播后,每一个内节点,尽管其可能包含的是一个运算符号,它也存储了以它为根节点的子树的运算结果。所以当对它的父节点作运算时,可以将它看作一个数字。所以方向传播的过程就变成了从根节点开始的,每一次算字节点的导数,最后导数累加的过程。这个过程希望读者可以自己来实现代码。
当读者实现完这个部分的代码后,一段完整的自动求导代码也就完成了。
本文作者 Auther:Soptq
本文链接 Link: https://soptq.me/2020/04/16/simple-autograd/
版权声明 Copyright: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明出处。 Content on this site is licensed under the CC BY-NC-SA 4.0 license agreement unless otherwise noted. Attribution required.
发现存在错别字或者事实错误?请麻烦您点击 这里 汇报。谢谢您!